拓扑优化方法目前在航空航天、汽车乃至于建筑领域都具有广泛的应用，本文将基于个人对拓扑优化方面的理解，进行一个简单的分类与介绍，希望能够帮助到刚刚开始相关领域学习的同学，文中有误之处也希望大佬指正。

（本人的研究方向主要偏向于拓扑优化与深度学习领域的交叉，将以这篇文章开始，简述本人关于这个新兴领域的理解与感悟）

对于刚刚接触优化领域的同学，可能首先需要了解的就是尺寸优化、形状优化与拓扑优化，对于这三种优化方法的不同点，可以通过1. 优化设计区域大小。2.是否产生几何的拓扑变形两个方面进行划分：

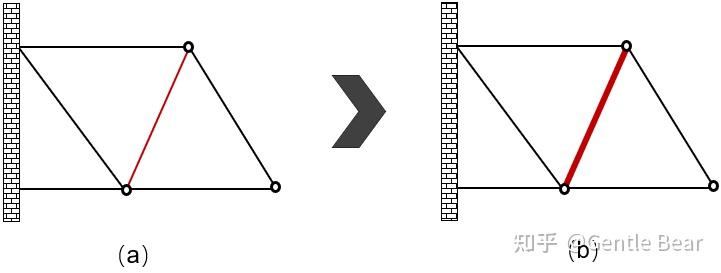
尺寸优化：对结构中某一个几何特征的尺寸进行寻优，从而获得某种更优的结构响应效果。例如下图中红色杆件尺寸的变化。

实际项目中实际项目中，尺寸优化通常作为拓扑优化后对特征尺寸精修的一个过程。由于问题具有离散特征，没有办法利用高效的梯度类型优化方法进行参数更新，因此尺寸优化通常采用一些遗传算法实现。可以采用软件二次开发，通过自己编遗传类算法实现、或者采用Isight软件直接进行寻优。

优化设计区域并非全局区域，而是对某具体特征的优化，且没有产生几何的拓扑变形。

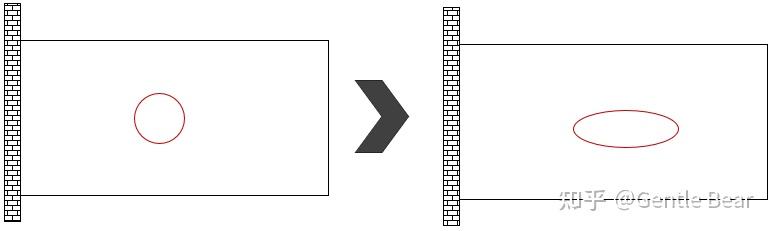
形状优化：形状优化是针对于结构中某一特征进行最优拓扑形状的寻找，如下图所示：对于形状优化我个人使用的比较少，感觉很像是局部的一个拓扑优化，可能拓扑结构的生成能力相对弱一些？

优化设计区域并非全局区域，而是对某具体特征的优化，产生了几何的拓扑变形。

拓扑优化：在载荷工况一定时，拓扑优化方法能够在设计区域内寻找最优的传力路径（最优的材料分布方式），从而将载荷传递到给定的支撑处，获得某种最优的结构性能。

拓扑优化的设计区域是全局性的（可自己定义区域），且结构整体会产生几何拓扑变形

传统的结构拓扑优化方法通常都伴随着结构的有限元网格离散处理、平衡方程求解、敏度信息获得与变量更新等步骤。自变量特性将影响各个环节所采用的求解方式，因此可以根据拓扑优化方法自变量类型将拓扑优化方法划分为基于连续体变量刻画的结构拓扑优化方法与基于离散体变量刻画的拓扑优化方法。

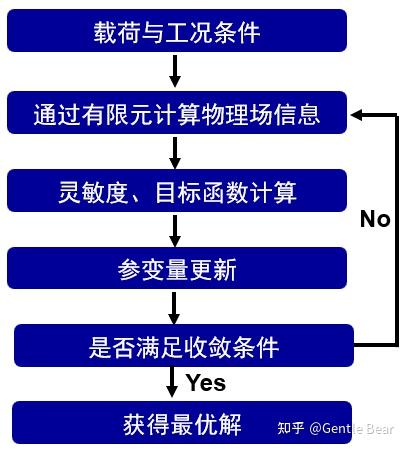
下文将根据优化方法的自变量类型对拓扑优化进行分类。

结构拓扑优化方法最早源于米歇尔[1]对桁架结构优化问题的研究，实现了对离散桁架结构单载荷工况下的结构优化分析，其工作后续也被称为米歇尔优化准则。

而基于米歇尔优化准则，通过引入数值方法实现了基于程序的高效优化计算，此类方法被统称为基结构法（Ground Structure Approach）。Zegard[2]与Tomasz[3]均公开了教育版代码。

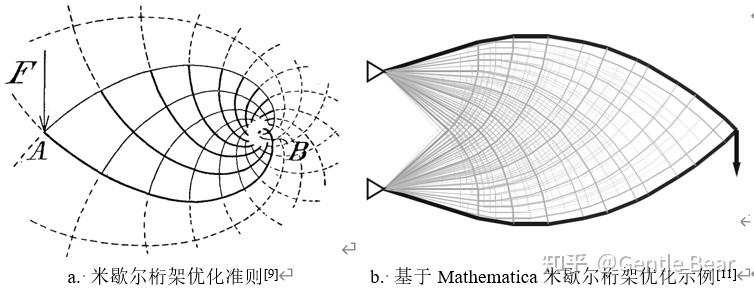
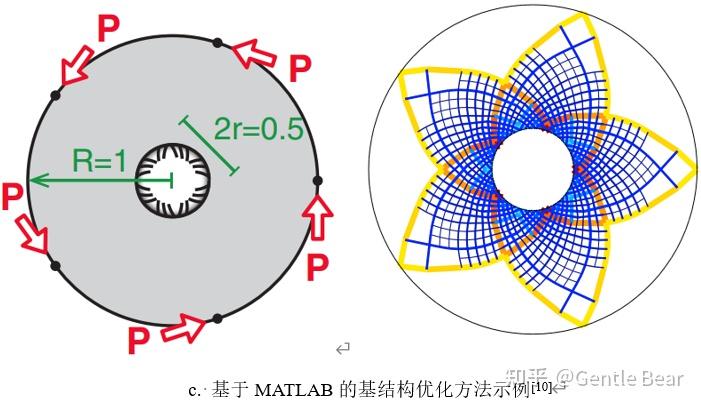
另一类学者通过主应力迹线（Principal Stress Line）[4]实现了类似于米歇尔桁架的结构优化，此类优化方法通常具有很高的计算效率，但是其对于三维问题、多载荷问题的适用性仍缺少足够的讨论。

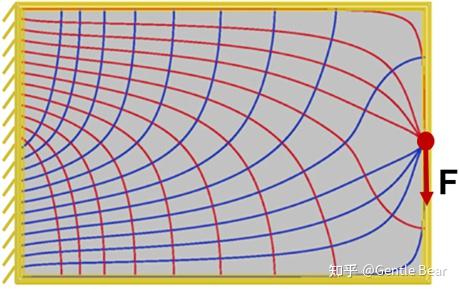
最后我将渐进结构优化方法（Evolutionary Structural Optimization, ESO）[5]纳入到了基于离散变量的拓扑优化方法中，包括后续发展的双向渐进结构优化方法（Bi-directional Evolutionary Structural Optimization）[6]。ESO/BESO方法的自变量为离散的有限元网格，以结构单元密度值的0或1代表结构材料的有无。ESO/BESO方法基于直观的工程逻辑思维，根据优化目标确定相应的优化准则，根据准则实现网格单元材料的增加与删除。

非常牛的是，刚刚举办世界杯的卡塔尔国家会议中心，就是通过此类优化方法提供基础设计建造的[7]

不同于离散体拓扑优化方法，连续体优化方法能够利用梯度信息实现自变量参数的更新。连续体结构拓扑优化方法按照对拓扑结构刻画方式的不同可以划分为人工密度单元类方法与边界演化类方法。人工密度单元法中固体各向同性材料惩罚法（Solid Isotropic Material with Penalization, SIMP）具有广泛的应用。

为避免离散体结构的0或1导致无法利用梯度信息的优化问题，SIMP方法通过引入惩罚因子将离散变量优化问题放松为连续体变量优化问题。而为了避免棋盘格现象、结构边界不清晰、网格依赖性问题，则提出再用过滤的手段进行处理。

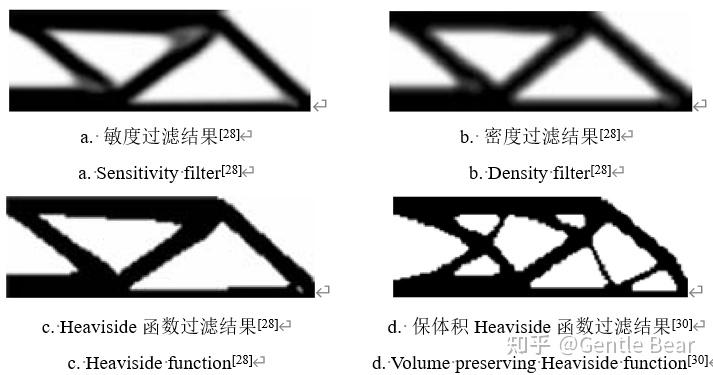
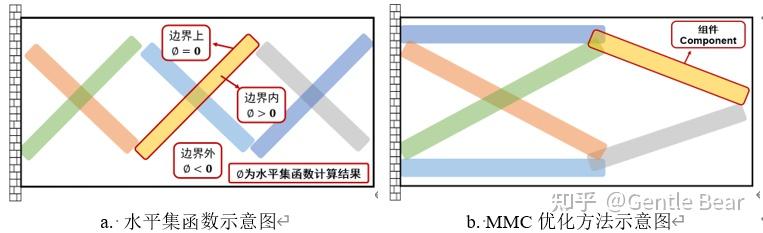
边界演化类优化方法通常基于水平集函数刻画结构边界。此类优化方法通常能够产生清晰的结构边界，不存在灰度单元问题。例如水平集优化方法（Level Set Method）以及可移动变形组件法（Moving Morphable Component, MMC）。

[1]Michell A G M. Limits of Economy of Material in Fram-Structures[J]. Philosophical Magazine, 1904, 8(47): 589–597.

[2]Dorn W. Automatic design of optimal structures[J]. J. deMecanique, 1964, 3: 25–52.

[3]Zegard T, Paulino G H. GRAND — Ground structure based topology optimization for arbitrary 2D domains using MATLAB[J]. Structural and Multidisciplinary Optimization, 2014, 50(5): 861–882.

[4]Gao G, Liu Z Y, Li Y Bin, et al. A new method to generate the ground structure in truss topology optimization[J]. Engineering Optimization, 2017, 49(2): 235–251.

[5]Xie Y M, Steven G P. A simple evolutionary procedure for structural optimization[J]. Computers and Structures, 1993, 49(5): 885–896.

[6]Young V, Querin O M, Steven G P, et al. 3D and multiple load case bi-directional evolutionary structural optimization (BESO)[J]. Structural Optimization, 1999, 18(2–3): 183–192.

[7]Biakowski S . Structural Optimisation Methods as a New Toolset for Architects[C]// 34th eCAADe Conference - Complexity & Simplicity. 2016.

我个人掌握有部分基础的优化代码，公开的资源我会免费提供给大家，我自己编写的代码可能会收取一丢丢的money作为劳动成本。无备注的都是Compliance优化问题

单尺度优化问题：

SIMP优化方法-2D-99行拓扑优化代码； SIMP优化方法-2D-88行拓扑优化代码（更高效）；

SIMP优化方法-2D-88行拓扑优化代码-采用敏度过滤/密度过滤/保体积Heaviside过滤；

SIMP优化方法-2D-99行拓扑优化代码-提取单元主应力、主应力方向（并绘制可视化图像）；

MMC优化方法-2D； MMC优化方法-3D； Level-Set方法-2D； MMC优化方法-散热问题；

SIMP优化方法-2D-基频优化； MMC优化方法-2D-基频优化；

基于满应力设计准则的桁架优化；

多尺度优化问题：

新渐进均匀化方法（NIAH，python）；　　　SIMP微观单胞设计；

等等还有一些....